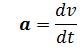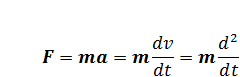前回、私たち誰もに共有な生存要件をもった個体を、「量子」や「素粒子」と並ぶ同列な一単位とみなし、《ヒューマン子》と名付けました。
むろんこの《ヒューマン子》という概念はきわめて抽象的なもので、物理学が対象とするような、特定の物的実体を対象とするものではありません。
私はしかし、それがそうした漠然とした概念でいいと考えています。むしろ、そうした相互浸透性をもったホーリスティック(全体的)な概念だからこそ、その可能性を持つものだと期待できます。
というのは、5章で述べたように、主観と客観あるいは科学と宗教といった、それまでの二元論的な物理学の枠組みが揺らぎ、また思想的には、西洋のそれと東洋のそれとの融合が静かに必要視されるといった、既成の学問的、思想的枠組や境界が問い直されてきたこの一世紀ほどの《時空認識》の変化に注目するわけです。言い換えれば、そうした旧来の学問的なり思想的なりの伝習を破って自在に羽ばたく、むしろ、そうした発想こそが必要とされていると思うからです。
さてそこで、この《ヒューマン子》という概念がもつ、もはや読者にはお馴染みの私の持論である「生活者」にからんだ、ある特色をあらためて強調したいと思います。
すなわち、《ヒューマン子》とは、観測される単位であると同時に、自ら自身を観測する存在であるという点です。これを「主客同体性」と呼ぶことにします。
一方、量子や素粒子というものは、外から《観測》されるのみの存在です。自ら自身を観測はしません。つまりこの「主客同体性」をもっていません。
しかしです、そうでありながら、上記のように最新の物理学の知見は、量子や素粒子が外からの観測では特定できない、これまた揺らぎをもった存在であることが明らかにしてきています。
いうなれば、《ヒューマン子》と「量子や素粒子」は、「主客同体性」をめぐって、その有と無という両端から、互いに接近しあってきているのです。象徴的な言い方をすれば、「意識」と「物質」とは、もはや互いに相容れぬ異世界の存在ではなくなってきているのです。
こうした「主客同体性」をめぐるその有無への気付きこそ、私がこの「新学問=反学問」とは「生活者」のためのものであるとする、その「生活者であること」の核心でもあることです。つまり、この「主客同体」で自在な存在であると同時に、そういう相互拘束な存在、それが《生活する》私たちの基盤にあるということです。
そこであらためて、いつもの三つの学問の場合の比較を振り返ってみます(下線部に注目を)。
《古典力学の場合》
1.自然における変化は連続量である。
2.物質の性格には大きく「波」と「粒子」の二つがある。
3.万物の世界を支配しているのは(古典)物理的な法則である。
4.物質の運動は、「運動方程式」で求められる。
5.物質は、初期状態を明らかにすればその運動(軌道)を決定できる。
6.物質の状態は、客観的事実であり、観測によって違いが生じるべきではない。
《量子力学の場合》
1.(量子は)とびとびの値をとる。
2.物質には、「波動と粒子の二重性」がある。
3.ミクロの世界を支配しているのは量子的な法則である。
4.物質の運動は、「波動方程式」で求められる。
5.物質は、空間的な広がりをもって確率的に存在する。
6.物質の状態は、観測されることによって変化する。
《新学問の場合》
1.人間の意識は「とびとび」に発展する。
2.人間の存在には、「二重性」が避けられない。
3.脳の神経細胞の世界の根底には量子的な現象がある。
4.意識の活動は量子的である。
5.意識は、多次元的な広がりをもって確率的に存在する。
6.意識の状態は、測定されることによって疎外される。
以上のうちの、各々の第1,2,3項についてはすで既述の章で議論してきた通りですが、それ以外、ことに第5と6項に関して、上記の私たち自身が《ヒューマン子》であり、「主客同体性」を持つ存在と、物理学という厳密科学の最先端の知見が示す微細粒子の測定ができない存在という、マクロとミクロの両世界における、互いに両極から歩み寄りつつあるという類似性に着目させられるわけです。そしてここに、「新学問」において「疎外」という視点が持ち込まれている理由が明瞭にされたかと思います。つまり、「観測されることによって変化する」という微細粒子の揺らぎと《ヒューマン子》という「相互拘束」な両存在に、「意識」と「物質」が異世界同士の存在ではないという「接近」を加えてとらえれば、そこに、「疎外」という心的現象レベルの境界的概念が生じてもおかしくない状態が浮かび上がってくるわけです。
むろん、こうしたマクロとミクロをまたぐ「類似性」が両世界の直接的な関係を示唆していると見るにはスケールが隔たりすぎています。しかし、そうではあるのですが、他方で、宇宙の誕生をめぐり、まさにミクロな物質の世界の探索がマクロな世界の解明への決定的な突破口となっているという、あたかもヘビの尻尾を探っているつもりが、それが頭の構造を明らかにしていたといった実際的到達があるわけです。すなわち、そうした極小の世界と極大の世界が、実は《結び合わさる環》であったとの発見であるわけです。
かくして、厳密科学の極致であったはずの理論物理学の世界にすら生じているこうした(あえて言いますが)“奇想天外”な発展を目の当たりにして、本新学問という生活上の実用世界においてならばなおさらに、相並ぶ「奇想天外」着想がもたらす気宇壮大な突破力に、大いに期待が託せるだろうと思うわけです。
そういう意味で、私たちの生活に、この《量子的ロマン》が、大いに花を咲かせてくれるであろうと展望し、それがこの「新学問」です。
さてそこで、上に指摘した「類似性」について、さらに踏み込んで、その手掛かりの度を数学手法の世界に確認してみたいと思います。
その方法は、図形、数式、あるいは座標を通して、その特殊化された表現からその意味する気配を嗅ぎ取ろうとする試みです。むろんそれらは対象現象の数学的代置表現で、それが対象自体にはなりえません。あくまでも探究のために考案された《道具立て》です。
しかし、そうではありながら、私たちの手足の延長としてのそれらは、いわば物質と精神の境界上に位置するものであり、そういう意味では、両世界を結ぶ媒体、あるいは、インターフェイスと見てよいものです。それを、職人が自分の使う道具の発するささやきを聞き逃さないように、あるいは、マラソンランナーがそのレース中、自分の身体と孤独な対話を続けながら走り抜くように、それらの手法に接してみることは可能です。
(ただ以下は、日常生活とはいかにも隔たった特定学問内の特異な議論への立ち入りであり、かつ、私による独自の解釈(あるいは曲解)を含んでいます。したがって、そうした逸脱には関われないとする向きにあっては、読み飛ばしていただいても結構です。)
非現実的な図形
まず初めに、「ぺンローズの階段」と呼ばれる図を見てみましょう。
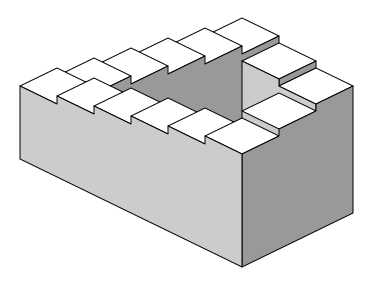
次は、「ぺンローズの三角形」と呼ばれる図です。
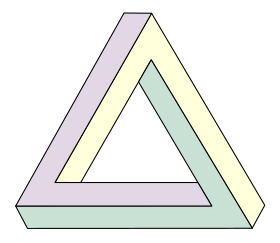
これらは、俗に「だまし絵」とも呼ばれるものですが、興味本位で見れば、ある種の視覚的錯覚を利用した“絵遊び”と言えます。
しかし、その本意とするところは、そういうものではなさそうです。
このペンローズというこれらの絵の考案者は、3章でふれた「量子脳理論」を提唱している(高齢ながら現存の)数学者、宇宙物理学・理論物理学者のロジャー・ペンローズのことです。つまりこれらの絵は、絵描きでもイラストレーターでもない著名厳密科学者が考案した、「あり得ないことがあり得る」との実例を、次元をまたぐ(ここでは二次元と三次元の間の)視覚的矛盾を利用して示して見せた絵と言えます。つまり、一方では、「常識を信用するな」との警告であり、他方では、「次元が変われば常識も変わる」との暗示です。
数式のパワー
上記の恒例の三比較中に、「運動方程式」と「波動方程式」という、二つの方程式の名が挙がっています。
そもそも「方程式」とは、等しいとされる二項目を、右辺と左辺にイコール記号で結んだものです。
たとえば、y =ax +b との方程式であるなら、y という変数は、 x という変数に、a と b という定数を加味したものと等しいという意味です。つまり、数学でない通常の文章表現中でいうなら、ある意味内容に特定の名称を付すとか、「すなわち」とかと呼び換える手法と同じことを、記号や厳密な約束事を用いて表現したものと言えます。
ここで例えば、a が 0.5、b が5、x が20 であった時、y は (0.5×20)+5 で15 となります。また、その両辺から同じ b を引いたものは同じはずで、y-b =ax となります。引くだけでなく、b を足しても、掛けても、割っても同じです。こうした関係を数式に表したものが「方程式」です。
そこでこの変数についてですが、その「変わりゆく」様子は、世の中に見てみれば、さまざまどころか無数にあります。上の y =ax +b との方程式は、そうした無数のもののうちの最も単純な変化、つまり、直線的な変化(グラフでいえば、下に記すように、直交座標上の一本の直線として表現される)をあらわしたもので、一次方程式と分類して呼ばれます。
さてそこで、古典物理学の場合の「運動方程式」なのですが、その説明の前に、私たちの身近な現象を見てみましょう。
たとえば車が走るつまり運動する場合、その移動距離を計算しようとすれば、距離=速度 × 時間、と頭に浮かびます。数式で書けば x =v×t です( x が距離、v が速度、t が時間)。
ただ、この場合の速度とは通常時速のことで、一時間当たりの速さです。むろん、速度には、分速もあれば秒速もあります。さらにそれを、もっと、もっと短くしていけば、極小時間中の瞬時の速度ということも考えられます。
この瞬時のことを求めることを「微分」といい、数式としては、両辺を時間 t で割ったかたちの、
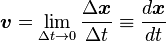 (単位例:km/hour)
(単位例:km/hour)
で表されます(この中辺は、△で表すx と t という二変数のうちの t をゼロにまでした極限という意味で、また ≡ 記号は定義するという意味で=と同じです)。ということは、速度 v とは、「動き」つまり「変化」の様子を瞬時の数値にして表したものということになります。この数値化によって、《変化の様子》が簡便に比較できるようにしたわけです(さもなければ、比較するには、いちいち、二台の車を走らせなければなりません)。
ところで、私たちが車を発進させる場合、アクセルを踏むと車は加速され、速度が上がります。つまり、そういう「速度」が連続的に変化しているわけです。そうした連続的変化の瞬間、瞬間での変化度を表すために加速度という概念を用い、今度は、距離でなく速度を時間 t で割ったかたちの(つまり微分して)、
ところが、この v は、 上式で x を微分したものでもありますのでこれを v に代入すると、
![]() となります。
となります。
この a が加速度(単位例:m/sec2 )です。
つまり、距離を時間で一度「微分」すると速度に、二度「微分」すると加速度になるわけです。
ちなみに、これらの関係を別なかたちで表すと、
x =v×t で、その v が a×t に等しいわけですから、その v を前式の v に代入すると、 x = (a×t)×t = a×t2 となります。
これを言い換えれば、移動距離は、加速度と時間の二乗をかけたものということとなります。そして、この変数の二乗に比例する関係を表す方程式を、二次方程式といい、グラフにすると、二次曲線(放物線)で表されます。
ところで、こうして車が加速されるには、それだけ、車のエンジンの出す力が加えられた結果です。そこで、その車の質量(重量)を m とすると、その力(F )は、
これが、古典物理学でいう 「運動方程式」です。
以上が、変化の様子を数値化して簡便化する数学的手法のあらましで、今日、私たちの日常世界でのいわゆる工学的計算は、こうした手法が縦横に使われているわけです。
ここで重要なことは、私たち人類は、こうした方程式を用いて、私たちの周囲の変化の様子を数値化する簡便法を考案し、文字通りフルに活用してきたということです。
さて、つぎが「波動方程式」ですが、下記のように、これはいっそう難物です。つまり、一つや二つの変数を扱うだけではなく、一度にいくつもの変数をあつかう手法であるということです。
まず、下の見慣れぬ記号「 ∂ 」とは、偏微分を表します。この偏微分の「偏」とは、ひとつの方程式にいくつもの変数が含まれている時、他の変数は変わらないとみなした上で、ある特定の変数だけをそれぞれに「微分」してみるという手法を意味します。つまり、下の波動方程式では、u という未知数は、t、x、y、z、の四つの変数によって表されることを意味する、三次微分方程式ということです。各記号の意味は、t は時間、x、y、z は三次元空間の各移動量で、 s は振動の位相速度です。
すなわち、ある瞬時 t におけるある位置の振動の変位を表す未知関数 u は、この式で表されるというものです。
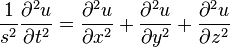
要するに、音や波や光の波動の一見複雑な「ふるまい」のすべてはこのたったひとつの式であらわされるわけです。
こうした方程式は、電気の発見によって推進された第二次産業革命にともない、19世紀、その電気、特に交流電流のふるまいを数値化するために考案されてきたものです。
そして、20世紀初頭に量子論が現れ、宇宙を伝わる光のふるまいを考察するなかで、アインシュタインの相対性原理が導かれてきたわけです。
座標のパワー
以上のような方程式の発達に合わせて発達してきた数学的手法に座標というものがあります。
その最もシンプルなものは、一本の直線に目盛りを付けたものです。もうほとんど、物差しと変わりはありません(おそらく座標の起源は、物差しにあったのでしょう)。ただし、ふつうの物差しに、マイナス値はありません。
下の数直線がそれで、x という変数の変化の状態をあらわします。そしてここでは、その上に x = 2 との例が表示されています。 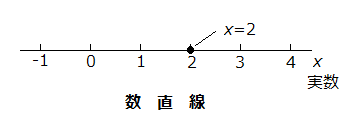
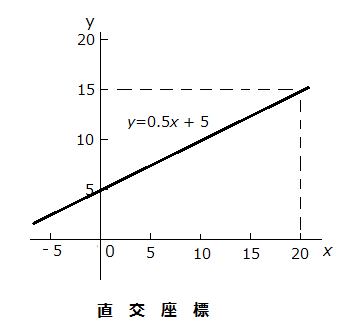
次に、下に示す図が直交座標と呼ばれるもので、x と y という、二つの変数からなります。 ここでは、上に例示した y = 0.5x + 5 という数式(一次方程式)をグラフ化してあります。
この直交座標に二乗の変数をもつ二次方程式をグラフ化すると、二次曲線(放物線)によってそれは表現されます。(つまり、上述の速度や加速度は、直交座標上では、加速度が放物線、速度がある特定の時点でそれに接する斜めの直線つまり勾配で表されます。)
ところで先に、この直交座標を用いて、東西文明の違いの特徴を表したことがあります(「東と西という座標軸」参照)。そうして、一見複雑に見える両文明の特色を、そう簡便化して特徴づけたわけです。そしてそれにはさらに、その両軸の交点(0点)に、垂直に立てた z 軸を加えて、三変数を持った関係のグラフ化を試みました。
以上のような座標軸の活用は、地上レベルの古典物理学に対応するもので、宇宙レベルの量子物理学には寸足らずです。
上に述べたように、電気の発見により、いっそう複雑な変数をもつ現象が対象となり、微分や偏微分といった、高度な数学手法が活用されてきました。そしてそれが、宇宙や量子といった極大と極小の世界の考察の必要にさらされる中で、いっそう高度な数学手法が開発されてきました。
そうした手法の発達の中で、当初は純粋な論理上の存在であった数学的概念が、後に、単に論理上での存在であるばかりでなく、現実の物理現象に適用する方程式を成り立たせる、論理と現実の橋渡しをするかの概念としても存在しうるようになってきたものがあります。それが「虚数」であり「複素数」です。
先に第一章の冒頭で、「物理学の世界に『物質』と『反物質』があるように、私たちが親しんできた常識の世界にもその『反対世界』があるようであり・・・」と述べました。また、私たちが実生活で遭遇する「疎外感」や「二重性」など、この世を“一重”の世界と想定していたのでは、とても対応しきれない現実感覚があります。そういう“反体性”を表す手法として、少なくとも数学上の概念に、そうした「虚数」や「複素数」があります。
そこで第二章で、「こうした逃れ難い「二重性」から自立してゆく、《 i 2 =-1》つまり「反学問」があるだろうとするものです」と述べ、数学上の虚数を借用し、かつ、拡大解釈して、そういう私たちの実存在を記号化してみたわけです。つまり、そういう簡便化です。
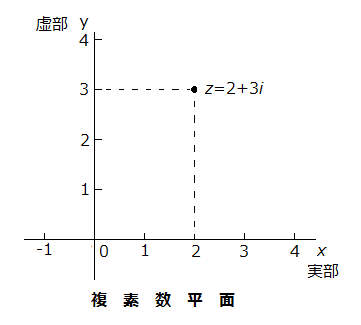
さて、そこで「複素数」ですが、これは、z = a + b i との式で表されるものです(z は複素数、a と b は実数、i は虚数)。これを座標化すると、以下のように表されます(注;以下の座標には、a が2、b が3、である例を書き込んであります)。
ただこの座標は、先にあげた「直交座標」とは違って、その x 軸は「実部」、y 軸は「虚部」と定義されています。(ちなみに、この「虚部」の「虚」とは、英語では imaginary と呼ばれ、「想像上の」という意味です。)
つまり、この座標「複素数平面」とは、x という実部の変数と、y という虚部の変数からなる「《二重》一次方程式」と言えるわけです。そしてこの「《二重》」とは、数学と現実とを橋渡しして、上記の私たちの実生活上の「二重性」にも沿えるものと想定できるのではないか、と私は考えています。
もちろん、こうした複素数平面とは数学上の概念で、私たちの現実の「平面」に直接対応するものではありません。
しかし、上に述べたように、速度や加速度が直交座標上で、直線や放物線で表されるように、私たちの「《二重》な世界」の“《二重》速度”や“《二重》加速度”も、この複素数平面での直線とか放物線とかとして、少なくとも、先の表現を再び使用すれば、「便宜上」の表現は可能となります。そこで、一種の“無理”は承知で、こうした数学上の概念を実生活上の概念と結び付け合わせると、例えばこの“《二重》速度”を「生活するスピード」とか、“《二重》加速度”を、「生活のスピードを上げる」とかとイメージすると、まんざら無関係でもなく、いかにも今日的な現実やその実感にそうものとなってくるのではないでしょうか。
実際の古典力学から量子力学への発展にあたって、その一歩々々の節目ごとに、そうした数式化や便宜化が行われ、その蓄積の結果として、上記のような波動方程式が導かれ、そしてそれが発展して今日の科学技術社会の礎となってきているわけです。
すなわち、波とは、私たち身近なところでは、水とか空気とか、その媒体の存在を前提としますが、その波、たとえば光が宇宙空間を伝わる場合、その空間は真空であり、媒体はありません。そのように、物理学の場を、平面から立体、そして宇宙へと発展させるその節目ごとに、次元を変えた方程式が考案され、ことに、宇宙空間という多次元な場を想定した理論において、複素数の概念抜きには、その方程式化はできませんでした。
率直に言って、私は、そうした数学的に極めて高度な数式上の発展の一歩々々をフォローできたわけではありません。しかし、私たちの実生活の毎日とは、宇宙空間でなされるわけでもなく、そうした高度数学の世界との直接な整合性が現実的に必要なわけではありません。そういう意味では、生活上は、疑似科学、それこそimaginary な存在で十分に有効であると考えます。
ただし今後の発展を考えますと、宇宙の誕生の解明と物質の微小粒子の解明が結合しつつあるように、私たちの意識と物質の関係の解明も、これまでの各章で述べてきたように、そうしたマクロとミクロの接点として、今後、達成されてゆくものと予想されます。
ましてや、死を境に、その前とその後の世界というものを考えますと(両生学講座「「未知多次元空間」と「移動生命体」参照)、明らかに、その後の世界とは、この地球を飛び出てゆくこともありえる微小物質の世界と考えられます。
最終章である次回、第七章では、そうした黄泉の世界を含め、「橋渡し」の問題を「奇想天外」に考察してみたいと思います。